无向图
无向图是图数据结构中最简单的一种，它通常使用 临接表数组 实现：
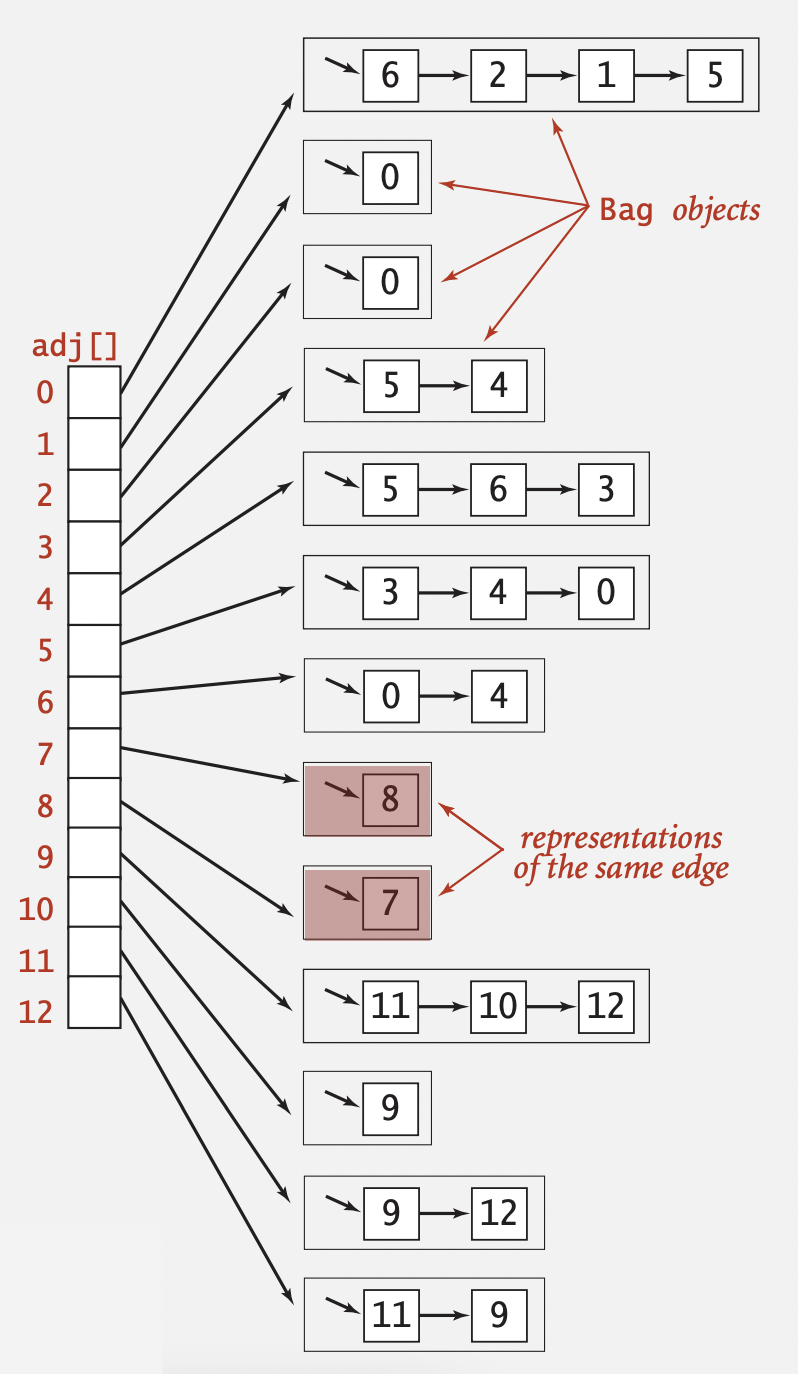
另一种高效方式是使用 临接矩阵 实现：
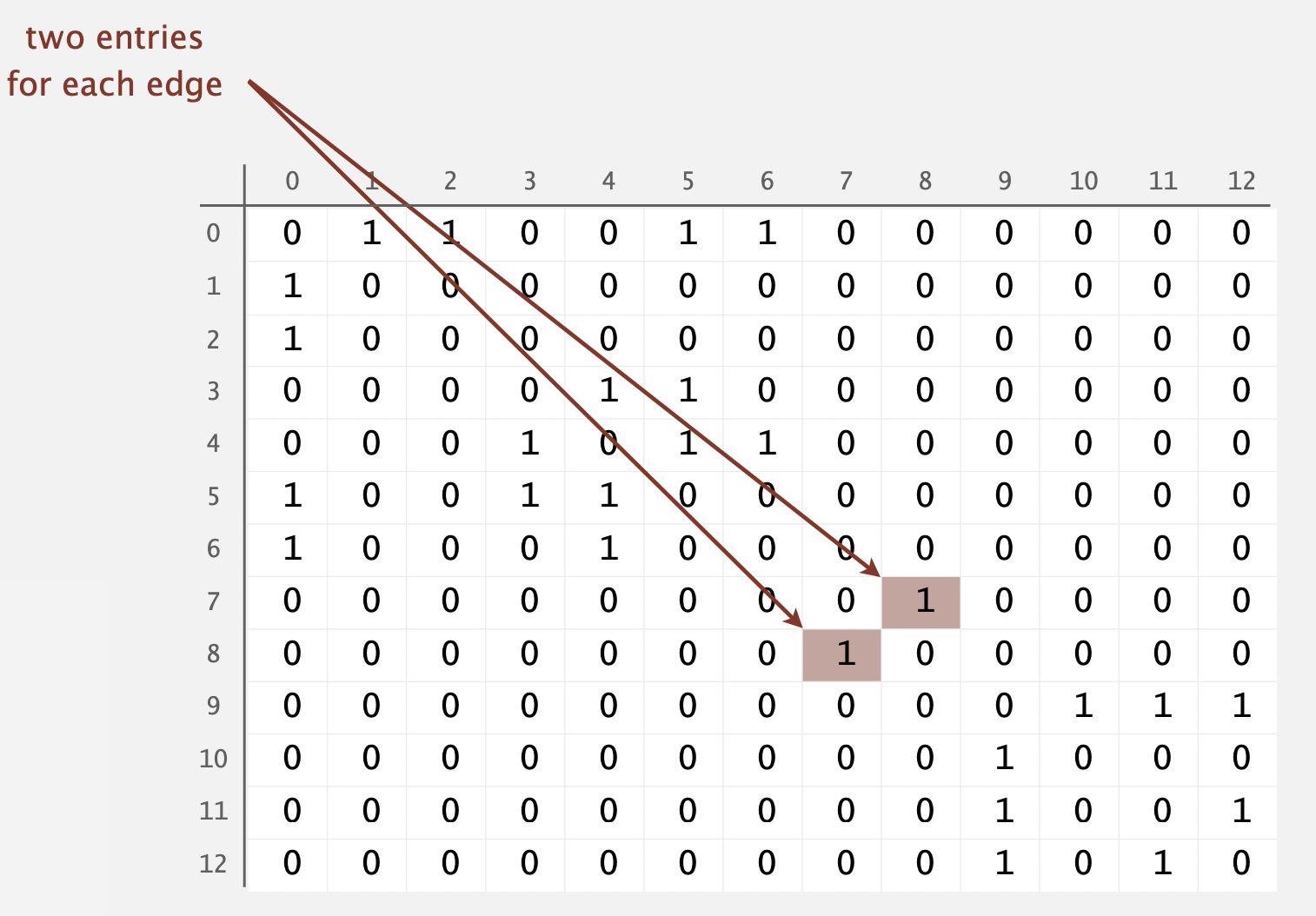
但 临接矩阵 有两个主要限制：
- 空间消耗较多，需要创建
nxn的矩阵，且创建后不易更改大小 - 无法表示
平行边
如果对于图的需求并不包含上述两个，那么 临接矩阵 不失为一种简单可行的办法。这里主要采用 临接表数组 来实现无向图。
临接表数组
临接表数组如上图，实现上非常简单：
class UndirectedGraph {
// Map 的 key 存储一个 `顶点`, value 存储该顶点的所有 `相邻顶点`
private store = new Map<number, number[]>();
}
DFS
搜索一张图最常规的方法是 DFS (Depth First Search)，DFS 也存在与树搜索中，树的 DFS 与图的 DFS 略有不同，但两者均为同一思想：尽可能深地搜索分支，直到该分支已到底才切换另一条分支。
无向图的 DFS 很简单，核心思路为：
- 任选图中的一个顶点，从该顶点( \(A\) )开始搜索
- 标记
\(A\)
为
已访问过 - 遍历该顶点(
\(A\)
)的的所有相邻顶点(
\(B_i\)
)，如果
\(B_i\)
未被
访问过，则从 \(B_i\) 重新开始搜索。
简单的代码表示为：
export class DFSSearch {
// 存储访问标记
private visitedMap = new Map<number, boolean>();
/**
* 创建搜索
* @param graph 图
* @param start 起点顶点
*/
constructor(protected graph: IGraph, protected start: number) {
this.dfs(start);
}
/**
* 从一个顶点开始dfs
* @param v 顶点
*/
private dfs(v: number) {
// 标记当前顶点访问过
this.visitedMap.set(v, true);
// 遍历顶点 v 的所有边，ev 是这条边的另一个顶点
for (const ev of this.graph.getAdj(v)) {
// 如果边的另一个顶点没访问过，则访问他
if (!this.visited(ev)) {
this.dfs(ev);
}
}
}
public visited(v: number) {
return this.visitedMap.has(v);
}
}