机器语言与汇编语言是何如工作的
前面几篇分别讲了计算机中的几种核心元件,通过这些基础元件我们可以实现更高级、更自动化的元件。而这些高级元件是靠什么来驱动呢?那就是电流,更准确的来说应该是一串高低电平序列,通过高低电平的不同组合,电路可以实现不同的逻辑,这也就是所谓的「机器语言」,对于人来说也就是一串01序列。由于一串01序列对人来说具有较差的可读性以及依赖硬件实现,所以人们在其之上创造了以「助记符」为核心的「汇编语言」。本文将试图说明机器语言和汇编语言的工作原理。
累加器
前面已经讲过了加法器,但是它只能处理两个数的加法,更多时候我们要进行多个数的加法,所以我们需要在加法器的基础上进行拓展,使整个结构能够不停的计算加法。
如果要连续进行加法计算,我们可以使用这样的方法进行计算:
- 计算第一个与第二个数的和
- 将上面的和存起来
- 计算第三个数与上面的和的和
- 将上面的和存起来
- 计算第四个数与上面的和的和
- 将上面的和存起来
- …
如果要计算 n 个数的和,那么只需不断的重复 「加和-保存」这个过程即可,这样的过程可以用下面的结构实现:
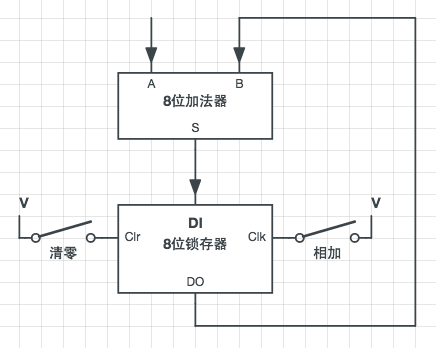
在计算开始前,首先将锁存器清零,这样锁存器默认的输出就全为0。接着输入第一个数,闭合相加开关,计算结果(第一个数与0的和,其实就是第一个数)就保存到了锁存器中,同时锁存器的输出又连接到了加法器的另一个输入。接着输入第二个数,闭合相加开关,第二个数与第一个数相加,其结果保存到锁存器中,并作为下一次加法的其中一个输入,接着输入第三个数,计算的就是这个数与前两个数的和的和,重复不断的进行输入,就能得到一大串数的和了。在上面的结构中,锁存器的作用就是存储计算产生的中间结果,所以锁存器在这里就称为「累加器」。
自动的累加过程
上面的加法器虽然可以正常工作,但是它有一个严重的问题:在计算过程中一旦输错了一个数字,那么必须把整个整个运算过程重复一遍。更好的办法是把前面构建的 RAM 与加法器连接起来,在 RAM 存储需要计算的数,这样修改起来就方便多了。而通过前一篇构建的计数器,我们可以让电路自动完成这些数的累加。
前面说过,要读或写某一个 RAM 单元是靠「地址」来定位的,例如000代表 RAM 的第一个存储单元,002代表第二个,通过地址我们能对 RAM 的任意地址单元进行操作。而对 RAM 地址进行遍历则要使用上一篇讲到了计数器,这是一个时钟信号驱动的能够输出有规律的二进制数的元件,这两个结合我们便可以把要计算的数依次存在 RAM 里,通过计数器遍历地址来输出每一个数,这样就能自动完成计算了。
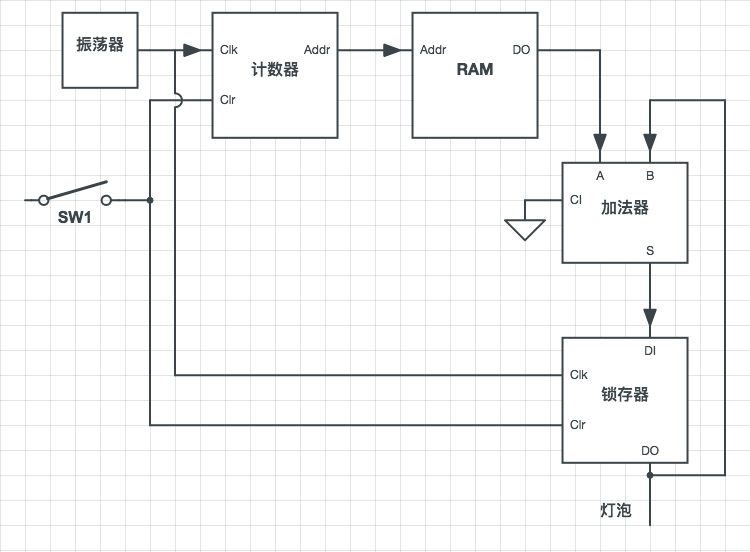
在使用前,首先闭合清零开关,此时锁存器输出及计数器输出均为0,导致RAM 也输出其第一个存储单元中的数据。接着断开清零开关,当振荡器第一次由0跳变至1时,发生下面两件事:
- 锁存器保存了 RAM 中第一个存储单元的值与0的和(累加器的第一步与第二步)。
- 将 RAM 的输出变为其第二个存储单元的值。
当振荡器第二次跳变时,锁存器保存 RAM 中前两个单元的值得和,同时RAM 输出为第三个单元的值。如此往复,电路就自动计算了 RAM 中存储的数的和。但是它也有一个问题,就是无法停下来。当计数器不断增加达到其最大值时,便会回滚至0,导致电路又把 RAM 中存储的数累加到已经计算出的结果中。
更加自动的累加过程
上面的电路可以一次计算若干个数的总和(例如:1+2+3+…+99),但假如我们要分别计算50对数的和(例如:1+2,3+4,5+6…),它就无能为力了,所以我们需要一种通用的机器,来进行更细粒度的计算,例如一次计算10个数,20个数,50个数的和。
上面的电路中,锁存器的输出连接至灯泡,用来显示 1次计算100个数的和的结果,但如果要分别计算若干对数的和,他就不是很方便了。更好的办法是将计算结果存储到RAM 中,这样在未来我们可以方便的查看计算结果。
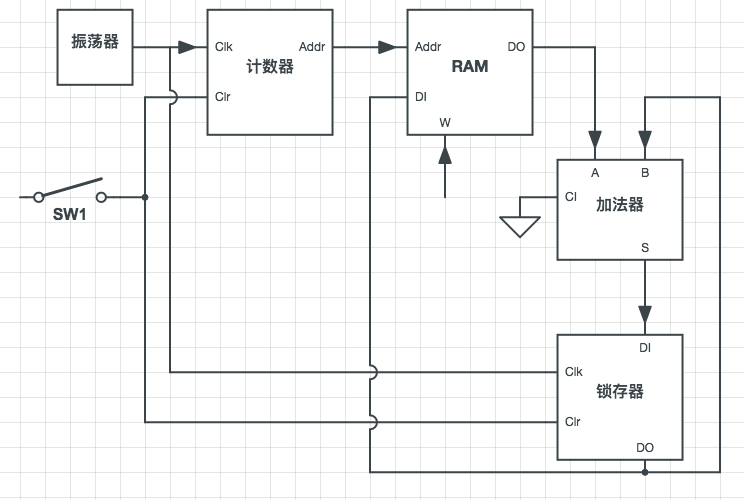
上面的电路中,将锁存器的输出连接至 RAM。在前面的手动累加过程中,RAM 中只存有要计算的数字,其存储单元如下所示:
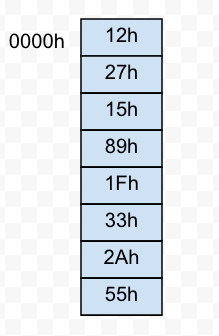
而在现在的电路中,要能实现一次对若干组数进行求和,就必须对 RAM 存储单元内的数据进行更改:
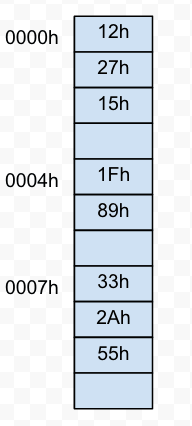
如上所示,存储单元中的数表示每组待计算的数,而存储单元的空白地方表示要存储前面的数的和,这些数据对应了下面的一串指令:
- 把0000h 地址处的数据加载到累加器
- 把0001h 地址处的数据加到累加器中
- 把0002h 地址处的数据加到累加器中
- 把累加器中的内容存储到00003h 处
- 把0004h 地址处的数据加载到累加器
- 把0005h 地址处的数据加到累加器中
- 把累加器中的内容存储到00006h 处
- 把0007h 地址处的数据加载到累加器
- 把0008h 地址处的数据加到累加器中
- 把0009h 地址处的数据加到累加器中
- 把累加器中的内容存储到0000Ah 处
- 停机
上面的存储单元仅存储了要计算的数据,但此时电路还不能正常工作,因为电路并不知道这些存储单元要参与什么运算,所以需要有一些代码来标记它们分别进行哪些操作。存放这些代码最简单的方法就是用另一个 RAM 来单独存储它,这两个 RAM 一个称为「数据段」,另一个称为「代码段」,它们应同时被访问。
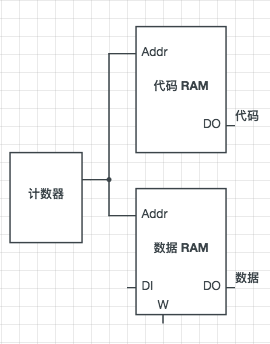
根据上面的数据端,我们发现需要有4中代码来标记每一步操作:
| 操作码 | 代码 |
|---|---|
| Load(加载) | 10h |
| Store(存储) | 11h |
| Add(加法) | 20h |
| Halt(停机) | FFh |
将数据端与代码段结合起来看:
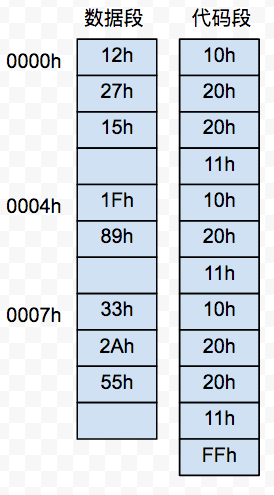
为了实现上面的 Load 功能,还需要对电路进行一些改造:数据段 RAM 的输出有时需要作为锁存器的输入,所以这里加入一个2-1选择器来实现。
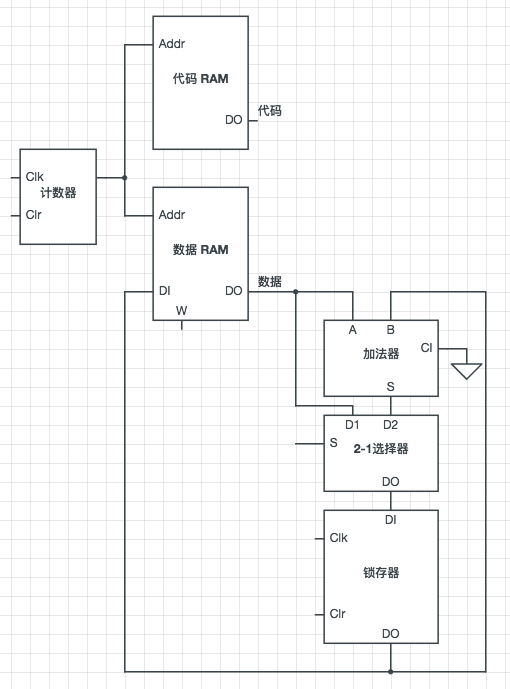
上图忽略了一些控制信号,例如清零、时钟、选择(S),其中一些明显是基于代码段 RAM 的输出,在这先暂时先忽略它们如何连接。
添加减法
上面的电路暂时只能进行加法运算,接着我们要对其增加减法功能,第一步是向操作码表中新增一个操作码:
| 操作码 | 代码 |
|---|---|
| Load(加载) | 10h |
| Store(存储) | 11h |
| Add(加法) | 20h |
| Sub(减法) | 21h |
| Halt(停机) | FFh |
回顾前面计算减法的一章,两个数的减法就是第一个数加上减数的补码,补码的计算方式就是按位取反后结果加1,在这里我们很容易将这一步加入到前面的电路中:
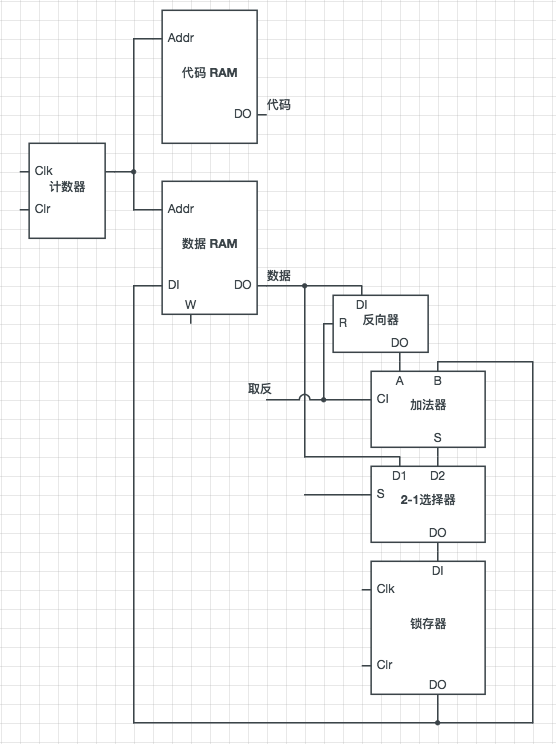
在这个电路中,在加法器前新增了一个反向器,用于对数据按位取反,同时控制是否取反的信号 R 与加法器的原始进位信号连接,当要计算减法时,该信号为1,导致反向器对数据取反并在加法器处加1,当计算加法时,该信号为0,数据保持原样输入至加法器,同时加法器不加1。
计算更高位的加法与减法
到目前为止我们的加法器及其连接的所有设备都是8位的,也就是说我们只能对两个8位二进制数进行计算,这样还是不太方便,我们需要能处理更高位的运算,例如16位的加法。一个简单的办法是将加法器及其所有连接设备均扩展至16位,但这样的成本就有些高,还有一种代价更小的解决方式,就是更改一下多位数的计算方法。
假设有两个16位数相加:76ABh + 232Ch。那么首先进行最右边的字节(低字节)加法:ABh + 2Ch = D7h,然后计算左边的字节(高字节)76h + 23h = 99h,最后两两个结果合并:99D7h,这就是 76ABh + 232Ch 的和。
这是最简单的情况,但有时两个16位数进行加法时,低字节可能会产生一个进位,例如 76ABh + 236Ch,低字节 ABh + 6Ch = 117h。要解决这个问题,我们需要在第一步计算低字节时用一个1位锁存器来保存这个进位(该锁存器称为进位锁存器),并作为高字节运算时的进位输入即可,同时还需新增一个操作码:「进位加法 (Add with Carry)」。当进行两个8位数加法时,仍采用普通的 Add 指令。当进行两个16位数加法时,低字节仍使用普通 Add 指令,其进位输出存储至进位锁存器(有进位为1,无进位为0),在进行高字节加法时,使用 Add with Carry 指令,加法器的进位输入使用进位锁存器的输出。
在8位减法中,进位输出通常为0,可忽略。而在16位减法中,低字节运算产生的进位输出应该保存在进位锁存器中,并作为高字节运算时加法器的进位输入,称之为「借位减法 (Sub and Borrow)」。
现在操作码表中又增加了两条指令:
| 操作码 | 代码 |
|---|---|
| Load(加载) | 10h |
| Store(存储) | 11h |
| Add(加法) | 20h |
| Sub(减法) | 21h |
| Add with Carry(进位加法) | 22h |
| Sub and Borrow(借位减法) | 23h |
| Halt(停机) | FFh |
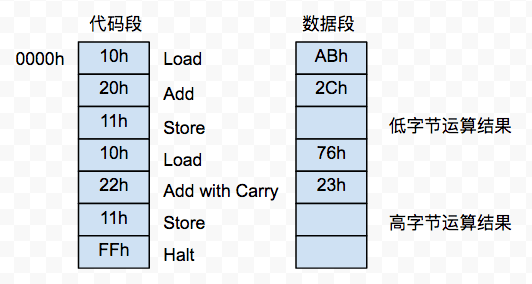
在进行多字节运算时,不论是否需要,运算至高字节处时都应该使用Add with Carry 或 Sub and Borrow。对于16位的加法,代码段和数据段是这样的:
非连续的寻址过程
前面的电路中已经实现了多位数字的加减法,但它还有个明显的缺点,就是后面的计算无法访问前面的计算结果。这是因为代码段 RAM 与数据端 RAM 是由同一计数器驱动,两者输出是同步、顺序的访问每一个地址。想象一下假如你的代码需要用到前面的一次运算结果,但这个结果已无法被访问,这就很蛋疼了。所以我们需要改造现有 RAM 结构,使其能够方便的访问任意地址。
在先前的电路中,每个操作码占一个字节,操作码操作的对象存储在数据段 RAM 中,由计数器将两者组合。现在我们将每个操作码扩充至 3 个字节,第一个字节为操作码本身,后两个字节表示操作码所要操作值在数据段 RAM 中的地址:
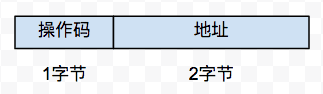
例如 Load 指令,它的第一个字节是其代码本身,后两个字节表示的是要加载到累加器的值的地址,这个地址可以是任意的。

上面的3个字节表示将0000h 处的值加载至累加器中。下面是一个完整的运算例子:

这里进行的是两个16位数的运算,首先计算其低字节,将结果存储至4005h,然后计算高字节,将结果存储至4004h。
要实现该设计的关键是把代码段 RAM 中存储的指令输出至3个8位锁存器中,每个锁存器表示指令的一个字节:第一个锁存器保存指令本身,第二第三个锁存器按高到低的顺序保存待操作的地址。
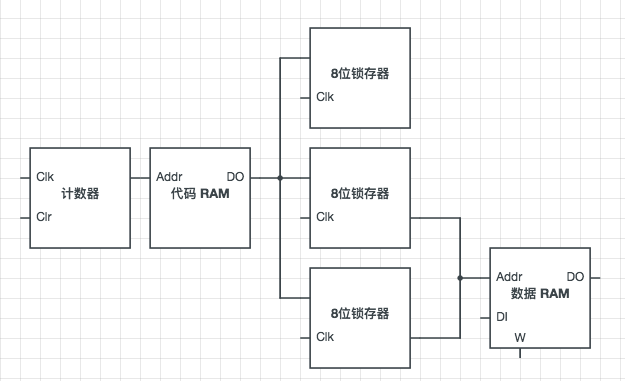
从 RAM 中取出指令的过程称为「取指令」,因为一条指令由3个字节构成,所以取出每条指令需3个时钟周期,加上执行需耗费1个周期,所以一条指令完成需4个周期。我们在这里实现了更方便的编码,但代价就是运行速度降低以及电路复杂度提升。
使用一个 RAM 实现
当电路实现了非连续的寻址方式,那么使用两个 RAM 就没有必要了。当时使用两个 RAM 是因为它们使用同一个计数器驱动来进行连续访问,既然现在实现了非连续访问,那么把代码段与数据段放在同一个 RAM 即可。
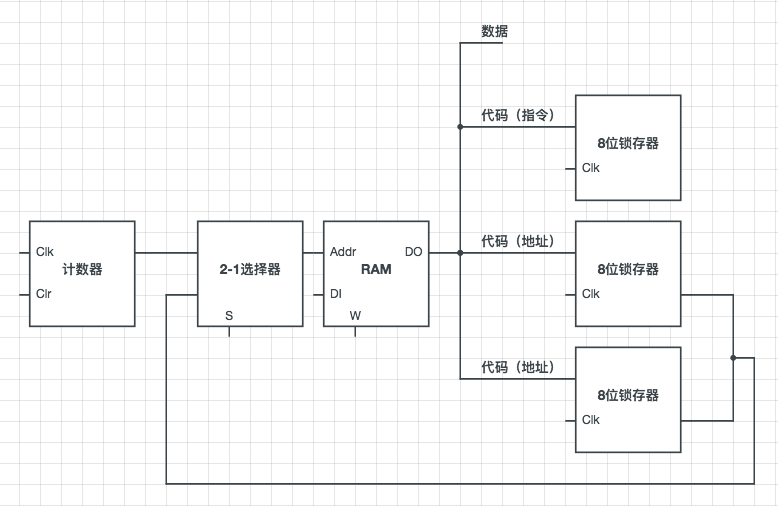
为了实现这个结构,在计数器与 RAM 见加了一个2-1选择器,用来选择是从计数器读取数据(用于取指令)还是从指令锁存器中读取数据(用于取数据)。
下面来看一下如何在这一个 RAM 中存放代码与数据:
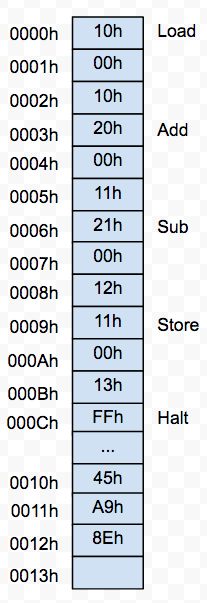
RAM 中的数据表示这里先进行2个8位数的加法,然后在结果中减去另一个8位数,最后将结果存储在0013h 处。
跳转
现在我们的电路已经可以实现非连续的寻址方式了,这为写代码提供了极大地便利,但仍有一些不足:仍以前面的代码为例,假设要在它的基础上再添加两个运算,这样得先把 Halt 指令移除,但这样可供写代码的空间还是不够,从原来 Hlat 的位置 000Ch 到 000Fh 仅有4个存储单元,这样就得把原来0010h处保存的数据后移,同时还得修改前面指令所指向的地址,这太麻烦了。
一个更好的做法是从0020h 处开始存放新的运算指令,这样就不影响前面的代码了。
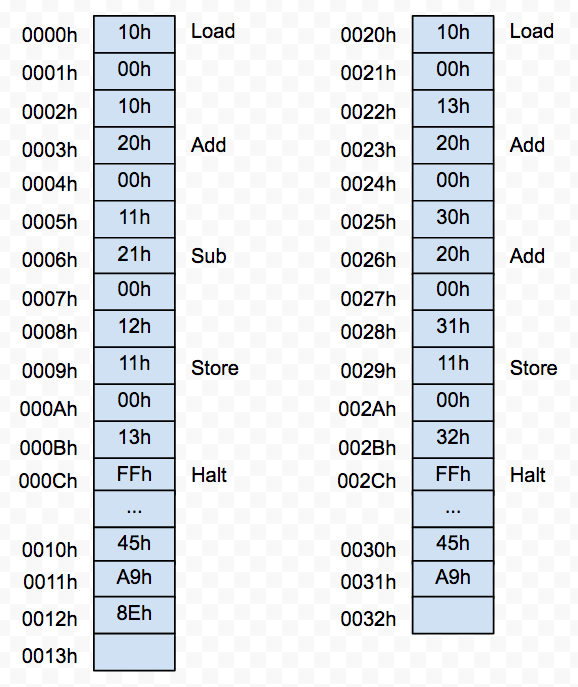
但这样的问题是两部分指令的其实地址分别为0000h 和0020h,前面的非连续寻址只是在读取数据时可以非连续,但每个就指令整体而言还是连续的,现在我们需要有一种方法来实现在指令级别上的跳转,这就诞生了 「跳转(Jump)」指令,通过 Jump 指令我们可以实现指令间的任意跳转,那这个指令该如何实现呢?
答案就是使用带预置和清零功能的 D 型边沿触发器。
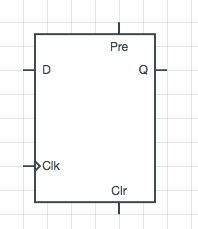
在正常情况下,Pre 和 Clr 都是0,但是当 Pre = 1时,Q = 1;当 Clr = 1时,Q = 0。除此之外与普通的触发器没有区别。这个触发器与计数器连接:
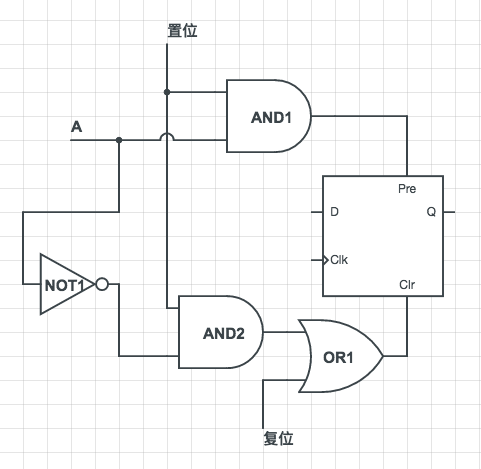
通常置位信号为0,在复位信号不为1时,清零信号也为0。当 A 为1时,则清零输入为1时,预置输入为1,如果 A 为0,预置输入为0,清零输入为1,这就意味这 Q 与 A 的值相同。通过这样,正常情况下,计数器自己不断改变,而一旦加载某一特定值,则从该值开始计数,这就实现了指令级别的跳转。这个锁存器只保存1位地址值,所以应当为计数器的每一位设置这样一个触发器,已达到整体设置特定值的目的,同时还要将锁存器的值连接至计数器:
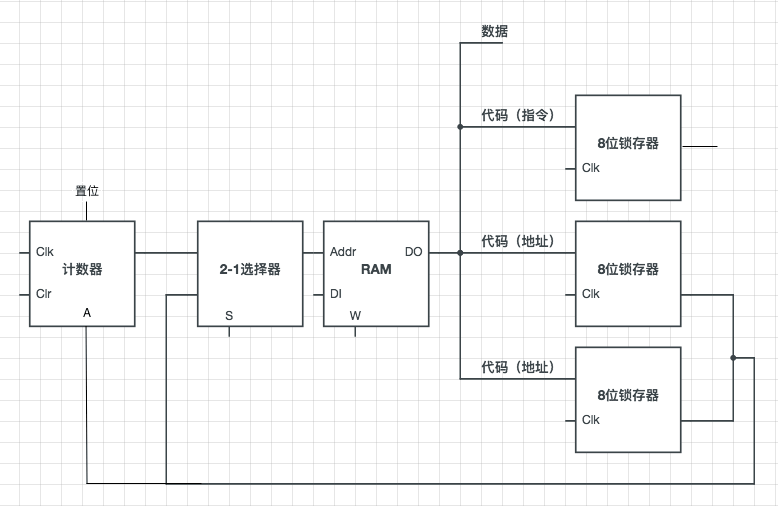
对于前面的代码,现在我们只要简单的改一条指令即可:
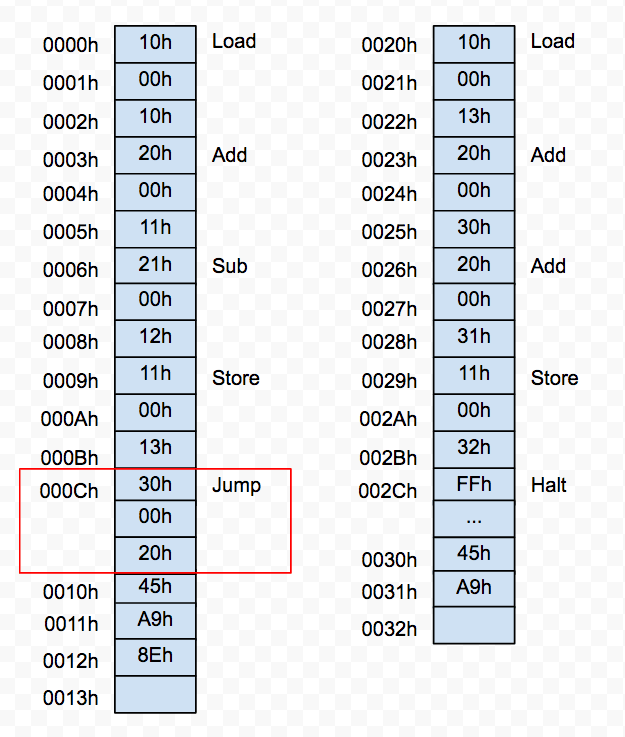
这里我们将 Halt 更改为 Jump,将跳转的地址指向了0020h,这样当程序运行到000Ch 时就会直接跳到0020h,直到遇到 Halt 停机。
条件跳转
前面的跳转不分场合,只要遇到就跳转。但有时我们需要在某些情况下才跳转,例如下面这个例子:
假设我们要计算 A7h 与1Ch 的乘积这该怎么做呢?首先大家都知道 A7h * 1Ch 就是把 A7h 连加 1Ch 次,所以我们可以这样计算:把 A7h 与自身相加,每次相加后给 1Ch 减一,如果在某次减一后原来的 1Ch 变成0,就说明已经连加 1Ch 次,此时停机,运算就结束了。运算的关键就是判断 1Ch 减一后是否变成了 0,这里我们需要引入:「非零转移 (Jump If Not Zero)」 操作码。那么它是如何实现的呢?
首先需要为加法器增加一个1位锁存器,它称为零锁存器。
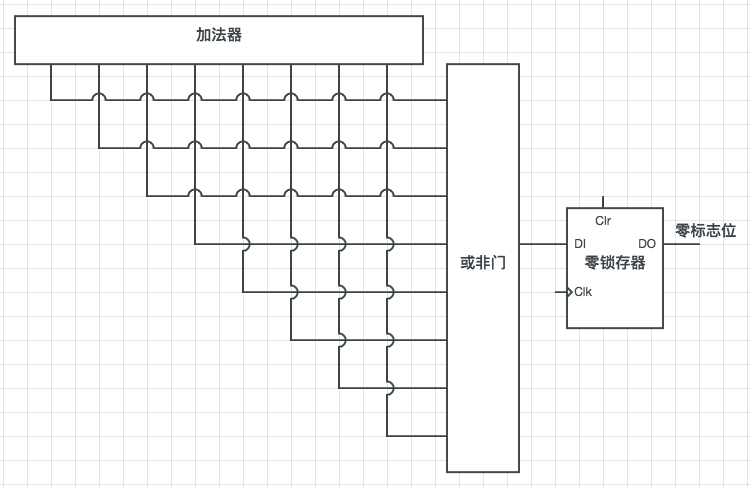
或非门的工作方式是只有当全部输入为0时才输出1,只要有一个1则输出0。当加法器输出为0时(各位均为0),零标志位为1,当加法器输出不为0时(有一位不为0),零标志位为0。
有了这个零标志位,我们就能知道上次运算结果是不是0,这样就能进行更多的判断。由此我们能扩展出新的几种条件跳转指令:
| 操作码 | 代码 |
|---|---|
| Load(加载) | 10h |
| Store(存储) | 11h |
| Add(加法) | 20h |
| Sub(减法) | 21h |
| Add with Carry(进位加法) | 22h |
| Sub and Borrow(借位减法) | 23h |
| Jump | 30h |
| Jump If Zero(零转移) | 31h |
| Jump If Carry(进位转移) | 32h |
| Jump If Not Zero(非零转移) | 33h |
| Jump If Not Carry(无进位转移) | 34h |
| Halt(停机) | FFh |
(其中有关进位的转移由进位锁存器与零锁存器共同实现)
有了非零转移指令,我们写乘法的代码就简单多了:
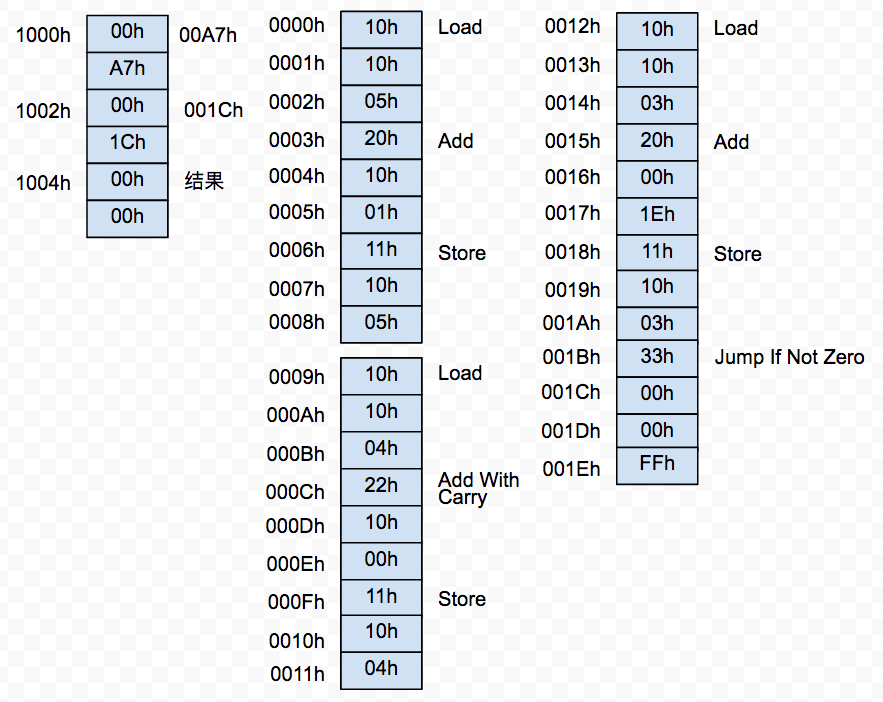
0000h 到 0011h 的作用是将 00A7h 与自身相加,0012h 到 0017h 是给 1Ch 加上 FFh(虽然 FFh 代表停机指令,但是它也是个合法的数字,这里就等于给 1Ch 减一),然后在 0018h 到 001Ah 将其存储。接着在 001Bh 判断上次给 1003h 处的字节加上 FFh 后其结果是否为0(Store 不影响零标志位),如果不为0,表示 1Ch 还没有变成0,则 00A7h 的连加还没有到1Ch 次,那就跳转到 0000h 再进行一次连加,如果为0,说明已经连加了 1Ch 次,此时不跳转,继续执行到 001Eh 停机,运算完毕。
数字计算机
到目前为止,我们构建的电路能够称为「数字计算机」,它的由四个部分组成:处理器、存储器、输入、输出。存储器就是那个 RAM 阵列,输入输出在电路中并未表示出来,但它确实是存在的,除此之外的设备都归类于处理器。处理器包含若干组件。例如累加器,虽然它只是一个锁存器。反向器与加法器构成了算数逻辑单元,即 ALU。计数器称为程序计数器。
软件
我们把电路结构及其元件称为硬件,而在 RAM 中存储的代码与数据称为软件。能够被处理器响应的操作码(例如 Load 指令的代码10h) 称为机器码或者机器语言。虽然计算机能轻易理解它但人不能,所以人们创造了助记符来描述特定机器码:
| 操作码 | 代码 | 助记符 |
|---|---|---|
| Load(加载) | 10h | LOD |
| Store(存储) | 11h | STO |
| Add(加法) | 20h | ADD |
| Sub(减法) | 21h | SUB |
| Add with Carry(进位加法) | 22h | ADC |
| Sub and Borrow(借位减法) | 23h | SBB |
| Jump | 30h | JMP |
| Jump If Zero(零转移) | 31h | JZ |
| Jump If Carry(进位转移) | 32h | JC |
| Jump If Not Zero(非零转移) | 33h | JNZ |
| Jump If Not Carry(无进位转移) | 34h | JNC |
| Halt(停机) | FFh | HLT |
助记符通常与其他一些字符结合使用
1ADD A, [1003h]
助记符右侧的 A 和 [1003h] 称为参数,其中 A 称为目标操作数,[1003h]称为源操作数,表示把1003h地址处的值加到累加器。使用这样结构表示的代码称为汇编语言,每一条汇编语句都对应机器码中的特定字节,就像 LOD 的机器码是 10h 一样。
到这里本文就结束了,回忆前面几篇文章,大体描述了一台计算机是如何工作的,虽然他非常原始,与现代计算机差距巨大,但原理还是与现代计算机类似的。