递归计算优化
递归在任何编程语言中都是重要的一部分,在Lisp中更是。一般递归可以分为三类:线性递归、树形递归与线性迭代。根据递归的定义,三者在函数体内都调用了自身,但不同的是线性递归与树形递归会导致时间与空间的指数级增长,而线性迭代的时间与空间增长是线性的。从表现上来说线性迭代比(线性/树形)递归会节省巨量的内存与运行时间,但(线性/树形)递归也不是毫无作用,它的程序表示非常清晰易懂,而复杂的线性迭代有时会难以理解。
线性递归 vs 线性迭代
线性递归的表示通常是非常通俗易懂的,可以说完全就是自然语言的程序化描述,例如阶乘的计算:
但它的缺点显而易见,运行时占用的内存空间与运行时间会呈指数级增长。分析一下函数的调用过程:
1(factorial 6)
2(* 6 (factorial 5))
3(* 6 (* 5 (factorial 4)))
4(* 6 (* 5 (* 4 (factorial 3))))
5(* 6 (* 5 (* 4 (* 3 (factorial 2)))))
6(* 6 (* 5 (* 4 (* 3 (* 2 (factorial 1))))))
7(* 6 (* 5 (* 4 (* 3 (* 2 1)))))
8(* 6 (* 5 (* 4 (* 3 2))))
9(* 6 (* 5 (* 4 6)))
10(* 6 (* 5 24))
11(* 6 120)
12720
每次进入一个新的递归过程后,调用栈都要保存现场,当计算的数值很大时,调用栈就会保存巨量的重复数据,这是程序占用空间暴涨的原因。
如果将程序改为线性迭代,程序的占用空间就立刻降下来了:
1(define (factorial n)
2 (fact-iter 1 1 n))
3
4(define (fact-iter product counter max-count)
5 (if (> counter max-count)
6 product
7 (fact-iter (* counter product)
8 (+ counter 1) max-count)))
它的运行过程为:
1(factorial 6)
2(fact-iter 1 1 6)
3(fact-iter 1 2 6)
4(fact-iter 2 3 6)
5(fact-iter 6 4 6)
6(fact-iter 24 5 6)
7(fact-iter 120 6 6)
8(fact-iter 720 7 6)
9720
clojure解释器是尾递归的,这才能确保是常数级别)。但显而易见线性迭代的代码不如线性递归的代码直观。
除了空间与时间上的优势,线性迭代的还有一个优势是可暂停的。例如上面线性迭代实现,每一次迭代参数只需要固定的三个值,那么我们只要固定存储这三个值,在程序中断后我们就能根据这三个值恢复任意一步计算。而线性递归虽然每一步参数数量也是相同的,但他还包含了大量的环境信息,那么这个恢复起来就复杂了。
那么线性迭代和线性递归到底是哪里出现了偏差呢?观察线性递归的递归表达式:(* n (factorial (- n 1))),该表达式不是以递归过程作为运算过程,而是将其做为+的参数,这就导致递归调用过程中始终包含大量环境信息。
而线性迭代的递归表达式(fact-iter (* counter product) (+ counter 1) max-count)中是以递归过程作为运算过程的,它不需要包含环境信息,返回值直接被用作当前函数的结果进行返回,也就是说它是“尾递归”的。这就是线性迭代高效的原因。
树形递归 vs 线性迭代
树型递归,顾名思义递归展开后就像一棵树一样,它与线性递归类似,但当递归表达式中包含多个递归过程自身调用后,线性递归就会变成树形递归。同线性递归一样,树型递归的优点在于易理解易描述,但缺点在于时间和空间的消耗会比线性递归还要多,以斐波那契数列的计算为例:
他的递归表达式中包含了两次自身调用,递归过程展开后是这样的:
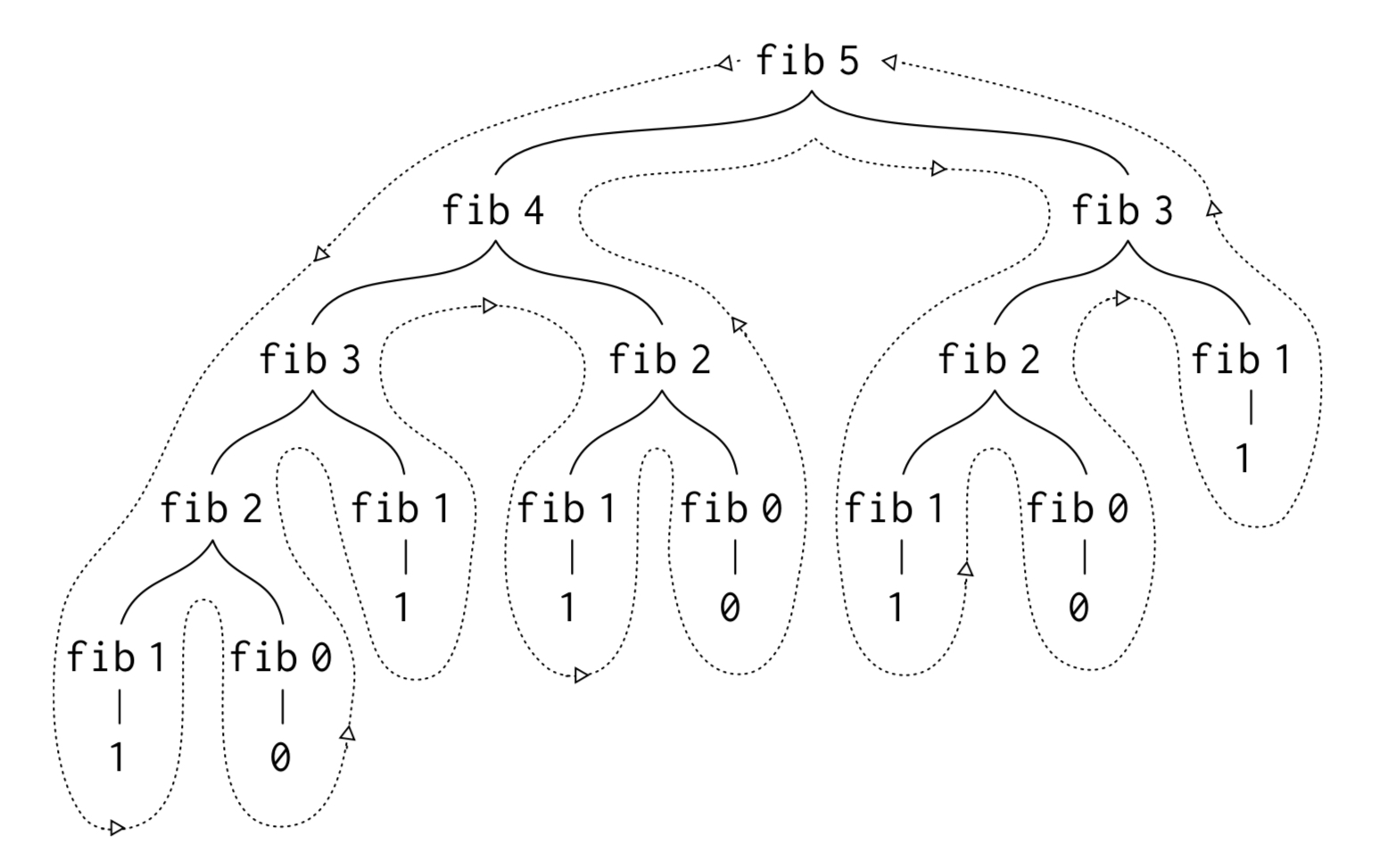
可以看到fib(3)的计算出现了2次,fib(2)的计算出现了3次,计算的值越高,重复计算的次数也就越多,这造成了时间与空间的暴涨。斐波那契数列计算可以简单的转化为线性迭代:
1(define (fib n)
2 (fib-iter 1 0 n))
3 (define (fib-iter a b count)
4 (if (= count 0)
5 b
6 (fib-iter (+ a b) a (- count 1))))
现在整个递归过程就变成线性迭代了,时间空间占用大幅缩短。
怎么将递归改成迭代
从上面的例子可以看出,迭代与递归的区别在于要将递归表达式改成递归过程自身的调用,而不能将其作为其它过程的参数,例如应该是(fib-iter (+ a b) a (- count 1))而不是+ (fib (- n 1)) (fib (- n 2))),那么怎么使用过程自身进行表达就是改造的关键。
一般来说,这个改造的过程伴随着计算过程的改造,简单来说,就是要找到原本递归过程中数据变化的规律,将这个变化规律用一个过程表达即可,下面以一个计算过程的改造为例。
函数 \(f\) 的定义为:
\[f(n)= \begin{cases} n& \text{n $<$ 3}\\\\ f(n-1)+2f(n-2)+3f(n-3)& \text{n $\ge$ 3} \end{cases}\]clojure表示:
1(define (calc n)
2 (if (< n 3)
3 n
4 (+ (calc (- n 1))
5 (* 2 (calc (- n 2)))
6 (* 3 (calc (- n 3)))
7 )
8 )
9)
那么这段代码的运行效率怎么样呢?这个树开了三个叉,显而易见时间空间消耗都远高于上面的斐波那契数列计算。使用DrRacket 7.6在i5-7500上运行,计算值为32,花费近1s。计算值为320,花费21min,时间上升近1260倍。如果计算数值继续增大,那恐怕地球毁灭了都算不出来。一个算法必须要能在可控的时间内返回结果,而它计算大数的时间已经是不可控的了,所以我们必须以迭代来改造它。
要想以迭代方式进行计算,首先我们需要找到迭代的计算规律:
\[f(3) = 1f(2) + 2f(1)\\\\ f(4) = 3f(2) + 5f(1)\\\\ f(5) = 8f(2) + 9f(1)\\\\ f(6) = 17(2) + 25f(1)\\\\ f(7) = 42(2) + 58f(1)\\\\ \dots\]可以看到,从$f(6)$开始,表达式中每一项的系数都是前三项分别于1,2,3乘积之和,例如:
\[17 = 8 + 2 \times 3 + 3 \times 1\\\\ 25 = 9 + 2 \times 5 + 3 \times 2\\\\ 42 = 17 + 2 \times 8 + 3 \times 3\\\\ 58 = 25 + 2 \times 9 + 3 \times 5\\\\\]clojure表示:
1(define (calc2 n)
2 (define (q a b c d e f count max_count)
3 (if (< count max_count)
4 (q (+ a (* 2 b) (* 3 c)) a b (+ d (* 2 e) (* 3 f)) d e (+ count 1) max_count)
5 (+ (* 2 (+ a (* 2 b) (* 3 c))) (+ d (* 2 e) (* 3 f)))
6 ))
7 (cond ((< n 3) n)
8 ((= n 3) 4)
9 ((= n 4) 11)
10 ((= n 5) 25)
11 ((> n 5) (q 8 3 1 9 5 2 6 n))
12 ))
这里n等于3,4,5时返回3个常数是因为迭代规律是从6开始的,3,4,5没有足够的迭代基础,所以可以直接返回常数,当n>5时,有了迭代基础,从这里开始进行迭代计算。
这段代码计算32时,耗时0.3s左右,计算320时,仍耗时0.3s左右。计算32000,耗时0.4s左右,可见时间上升非常缓慢,同时内存占用也比递归版本低很多。
上面是一个简单的例子,但并不是所有递归过程都这么好改。对于纯数值计算,最好能将递归改成迭代,这样可以节省很多时间与空间,但有些递归过程却没有这个必要,例如编译过程中语法树的遍历,它并不是纯计算的过程,并且遍历过程中本身就要存储一些信息到调用栈中,所以并不是所有递归都有必要进行迭代优化,需要根据实际场景选择。