减法是如何运算的
上篇文章说到了数字电路计算加法使用「加法器」,那可能你会自然的想到做减法当然是用减法器,然而事实却不是,计算减法仍然用的是加法器,这与负数在在二进制下的表示有关。
为什么没有专门的减法器
想一下人是怎么做减法的?假如有 673 - 396,首先最右边的 3 - 6 不够,需要向前一位「借位」,就是 13 - 6 = 7,7 被借了一位得 6,6 - 9 还是不够,又得向前借位,就是16 - 9 = 7,6 被借了一位得 5,5 - 3 = 2,所以答案就是277。在整个运算过程中涉及到了复杂的借位,这是比加法的进位复杂的多的过程,如果按这种方式实现电路会比现有解决方案复杂的多。
补码
那该如何实现呢?答案就是使用补码。假设有数字6,那么 -6 就可以表示为 0 - 6。同样假设有四位二进制数 0100 ,则它的相反数可以表示为 0000 - 0100,因为被减数小于减数,所以被减数要向上借一位得 10000,所以就是 10000 - 0100,而 10000 又可以写成 1111 + 1,所以 10000 - 0100 就变成了 1111 - 0100 + 1,而其中的1111 - 0100 实际上就是对 0100 的每一位取反,得 1011。所以最后的结果就是 1011 + 1 = 1100,而 1100 就是 0100 的相反数,而它就是 0100 的「补码」。
综上,我们可以总结一下二进制数的补码的计算方式:
- 对二进制数的每一位取反
- 给取反后的结果 + 1
计算减法
可能你会觉得补码这个东西用在运算中可能不太直观,而事实上这是遵循以往我们学过算术的。10 - 6 就可以表示为 10 + (-6),也就是A - B等于 A + B的相反数,而补码相对于一个二进制数来说就是它的相反数,所以逻辑上是通的。理清了计算的原理,下面来详细的看一下实际是如何运算的。
假设有如下两个4位二进制数 0110 - 0101。首先计算 0101 的补码,得1011,现在就变成了0110 + 1011 = 10001,由于这是4位二进制运算,结果为5位,所以最高位溢出则忽略,所以最终结果就是0001,这个结果是正确的。
上面是被减数大于减数得情况,下面我们把上例两个数字颠倒,看一下被减数小于减数得情况,就是 0101 - 0110。首先求 0110 的补码为1010,现在就变成了0101 + 1010 = 1111,由于并没有溢出,所以1111就是最终结果。
电路
现在我们已经知道减法是如何计算的了,下面来看一下电路该如何搭建。由于前面说过使用补码得好处就是仍然可以用加法器来计算减法,所以能计算减法得电路仍是在加法器得基础上的。回顾下前面得计算方法,我们需要将加法器进行如下改造:
- 需要接收一个信号来判断计算加法还是减法
- 如果计算减法,使电路能够计算补码
- 判断结果是否溢出
计算补码有两步:取反,加一。我们可以把取反与第一步结合起来,只有当计算减法的信号(下称sub)为1时才取反,这个可以用一个异或门来解决:
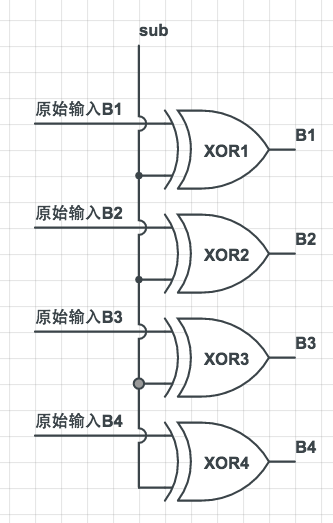
我们可以称其为「求补器」。现在解决了取反的问题,那还有个加一呢?看下前面的加法器结构:
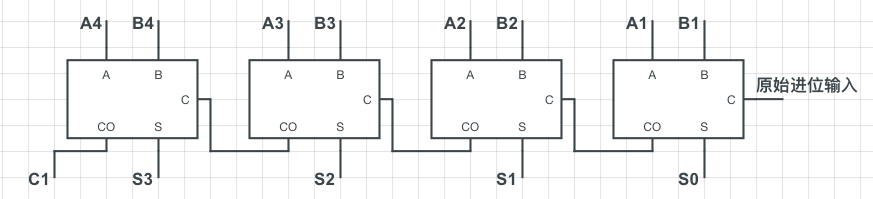
现在将原始进位输入改为sub,当要计算减法时,sub为输入1,既可以通过求补器将原始输入取反,又可以直接加一,当要计算加法时,sub 输入为0,此时通过求补器原始输入保持不变,原始进位输入也为0,下面是改造后的加法器:
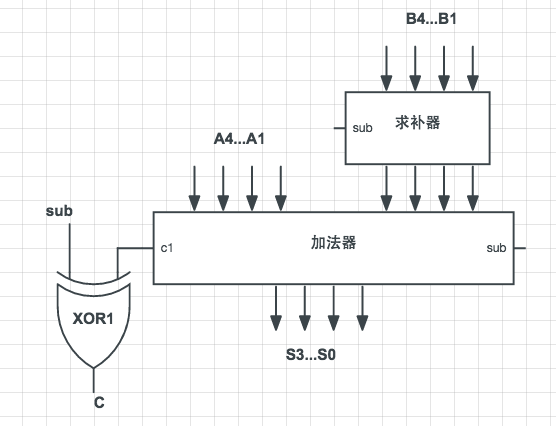
c1与sub共同作为输入来进行运算,输出的结果c将表示运算结果是否上溢/下溢。当计算减法时,sub输入为1,如果减数大于被减数,则会得到一个负数,此时c1为0,C将会输出1,表示下溢。当计算加法时,如果得到的数字大于255,C也会输出1,此时表示「上溢」。
带有减法功能的加法器到这里就差不多了