Z

三维变换

旋转矩阵及其逆矩阵

从前面的变换我们知道一个旋转 θ\theta 角度的变换矩阵是这样的

Rθ=(cosθ−sinθsinθcosθ)R_{\theta } =\begin{pmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{pmatrix}

但如果是一个旋转 −θ-\theta 角度的变换呢？我们可以用 −θ-\theta 来代替 θ\theta ，通过三角函数诱导公式我们可以得出

R−θ=(cosθsinθ−sinθcosθ)=RθTR_{-\theta } =\begin{pmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{pmatrix} =R^{T}_{\theta }

即 −θ-\theta 的变换矩阵是 θ\theta 变换矩阵的转置。同时从数学定义上来说， R−θR_{-\theta } 与 RθR_{\theta } 是互逆的矩阵，即

R−θ=Rθ−1R_{-\theta } =R^{-1}_{\theta }

所以旋转矩阵的逆等于旋转矩阵的转置，如果我们想求一个旋转 −θ-\theta 角度的矩阵，那么只要得到旋转 θ\theta 角度的矩阵的转置即可

RθT=Rθ−1R^{T}_{\theta }=R^{-1}_{\theta }

在数学上如果一个矩阵的逆等于他的转置，那么这个矩阵称为正交矩阵。

在三维的齐次坐标体系下，旋转矩阵会比二维复杂一些，但总的来说依然是对二维的扩展

Rx(α)=(10000cosα−sinα00sinαcosα00001)R_{x}( \alpha ) =\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & cos\alpha & -sin\alpha & 0\\ 0 & sin\alpha & cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} Ry(α)=(cosα0sinα00100−sinα0cosα00001)R_{y}( \alpha ) =\begin{pmatrix} cos\alpha & 0 & sin\alpha & 0\\ 0 & 1 & 0 & 0\\ -sin\alpha & 0 & cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} Rz(α)=(cosα−sinα00sinαcosα0000100001)R_{z}( \alpha ) =\begin{pmatrix} cos\alpha & -sin\alpha & 0 & 0\\ sin\alpha & cos\alpha & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}

旋转分解

前面几个例子都是绕轴旋转，而更常见的旋转可能是任意方向的旋转，例如极限竞速地平线中我们可以对改装好的车进行任意角度的旋转来预览改装效果。与之前的组合变换类似，旋转也是可以组合的

Rxyz(αβγ)=Rx(α)Ry(β)Rz(γ)R_{xyz}( \alpha \beta \gamma ) =R_{x}( \alpha ) R_{y}( \beta ) R_{z}( \gamma )

那么问题来了：我们可以将旋转组合为一个旋转矩阵，但如果有一个旋转矩阵，我们怎么将其分解为三个轴上的旋转呢？答案是使用「Rodrigues’ rotation formula」 。

R(n,α)=cos(α)I+(1−cos(α))nnT+sin(α)(0−nznynz0−nx−nynx0)⏟NR(\boldsymbol{n} ,\alpha ) =cos( \alpha ) I+( 1-cos( \alpha ))\boldsymbol{nn}^{T} +sin( \alpha )\underbrace{\begin{pmatrix} 0 & -n_{z} & n_{y}\\ n_{z} & 0 & -n_{x}\\ -n_{y} & n_{x} & 0 \end{pmatrix}}_{N}

它表示过原点的方向（向量） n\boldsymbol{n} ，旋转了 θ\theta 角度后的结果。

视图变换（模型视图变换）

我们在显示器上看到的图像都是二维的，而这个二维图像是从三维空间中投影到二维平面中的，想象一下生活中拍照的过程，就是将三维空间中的图像映射到二维平面中。图形学里也有相机的概念，它是定义映射方向的过程，与现实生活中拍照找角度是类似的。

进行视图变换，首先我们需要定义观测方向，也就是相机如何摆放，相机方向的定义由三部分组成：

  • 相机的位置 e⃗\vec{e}
  • 相机的观测方向 g^\hat{g}
  • 相机的向上方向 t^\hat{t}

相机与被观测物体只要相对位置相同，那么观测结果肯定是一样的，

所以为了方便起见，也是约定俗成，我们总是将相机放在原点 (0,0,0)(0, 0, 0) ，并且相机的向上方向总是 YY 轴，观测方向为 −Z-Z ，将这个变换过程记为 MM ，因为需要保证相对位置相同，所有被观测物体也都需要应用这个变换过程。

这个位置称为相机的标准位置。那么怎么将相机从任意位置转换到标准位置呢？

假设原本相机位置为 e⃗\vec{e} ，观测方向为 g^\hat{g} ，向上方向为 t^\hat{t} ，我们要将相机位置挪到标准位置，首先将 e⃗\vec{e} 做平移挪到原点，然后旋转 g^\hat{g} 到 −Z-Z ，最后将 t^\hat{t} 旋转到 YY 就行了，下面就可以根据之前的只是来写这些变换矩阵了。

首先是平移变换，因为转换的过程第一步就是平移相机位置，它非常好写

T=(100−xe010−ye001−ze0001)T=\begin{pmatrix} 1 & 0 & 0 & -x_{e}\\ 0 & 1 & 0 & -y_{e}\\ 0 & 0 & 1 & -z_{e}\\ 0 & 0 & 0 & 1 \end{pmatrix}

因为平移方向是从非原点到原点的，所以平移矩阵的平移量都是负向量。接着来考虑旋转变换，要将 g^\hat{g} 旋转到 −Z-Z ， t^\hat{t} 旋转到 YY ， (g^×t^)(\hat{g}\times\hat{t}) 旋转到 XX ，但将任意一个向量旋转到一个轴上不太好写，所以我们可以先考虑反着写，将具体的轴旋到对应向量上

R−1=(xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001)R^{-1} =\begin{pmatrix} x_{\hat{g} \times \hat{t}} & x_{t} & x_{-g} & 0\\ y_{\hat{g} \times \hat{t}} & y_{t} & y_{-g} & 0\\ z_{\hat{g} \times \hat{t}} & z_{t} & z_{-g} & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}

来验证一下，通过这个矩阵，我们要进行三个操作：

  1. 将 XX 轴旋转到 (g^×t^)(\hat{g}\times\hat{t}) 上
(xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001)(1000)=(xg^×t^yg^×t^zg^×t^0)\begin{pmatrix} x_{\hat{g} \times \hat{t}} & x_{t} & x_{-g} & 0\\ y_{\hat{g} \times \hat{t}} & y_{t} & y_{-g} & 0\\ z_{\hat{g} \times \hat{t}} & z_{t} & z_{-g} & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 1\\ 0\\ 0\\ 0 \end{pmatrix} =\begin{pmatrix} x_{\hat{g} \times \hat{t}}\\ y_{\hat{g} \times \hat{t}}\\ z_{\hat{g} \times \hat{t}}\\ 0 \end{pmatrix}
  1. 将 YY 轴旋转到 t^\hat{t} 上
(xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001)(0100)=(xtytzt0)\begin{pmatrix} x_{\hat{g} \times \hat{t}} & x_{t} & x_{-g} & 0\\ y_{\hat{g} \times \hat{t}} & y_{t} & y_{-g} & 0\\ z_{\hat{g} \times \hat{t}} & z_{t} & z_{-g} & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 0\\ 1\\ 0\\ 0 \end{pmatrix} =\begin{pmatrix} x_{t}\\ y_{t}\\ z_{t}\\ 0 \end{pmatrix}
  1. 将 ZZ 轴旋转到 −g^-\hat{g} 上
(xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001)(0010)=(x−gy−gz−g0)\begin{pmatrix} x_{\hat{g} \times \hat{t}} & x_{t} & x_{-g} & 0\\ y_{\hat{g} \times \hat{t}} & y_{t} & y_{-g} & 0\\ z_{\hat{g} \times \hat{t}} & z_{t} & z_{-g} & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 0\\ 0\\ 1\\ 0 \end{pmatrix} =\begin{pmatrix} x_{-g}\\ y_{-g}\\ z_{-g}\\ 0 \end{pmatrix}

可以看到都没问题，将轴旋转到某一方向很好写，这比将某一方向旋转到轴上容易理解多了。现在我们实际要求的旋转矩阵的逆矩阵已经写出来了，该如何得到我们想要的旋转矩阵呢？前面提过，旋转矩阵是正交矩阵，那么旋转矩阵的逆就是它的转置，所以我们最终想要的旋转矩阵就是

R=(xg^×t^yg^×t^zg^×t^0xtytzt0x−gy−gz−g00001)R=\begin{pmatrix} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0\\ x_{t} & y_{t} & z_{t} & 0\\ x_{-g} & y_{-g} & z_{-g} & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}

最后，总的视图变换矩阵就是

M=RTM=RT

总结一下，视图变换是将任意相机（包含位置、观测方向、向上方向三个属性）变换到标准位置（相机位置在原点，向上方向为 YY 轴，观测方向为 −Z-Z 轴）的变换过程，为了保持相机与被观测物体的相对位置不变，被观测物体也要应用这个变换过程。

因为视图变换针对的是相机，但是为了保持被观测物体与相机的相对位置不变， 被观测物体也要应用这个变换，也就是说对被观测物体应用这个变换后，相机一定是在标准位置的，所以模型变换与视图变换经常被放在一起，称为模型视图变换。

投影变换（正交与透视）

投影分为两种：

  • 正交投影
  • 透视投影

对一个立方体进行两种投影，可以看到正交投影的结果中每条线仍是保持平行或垂直的，没有发生形变，而透视投影发生了形变，有了近大远小的视觉效果。

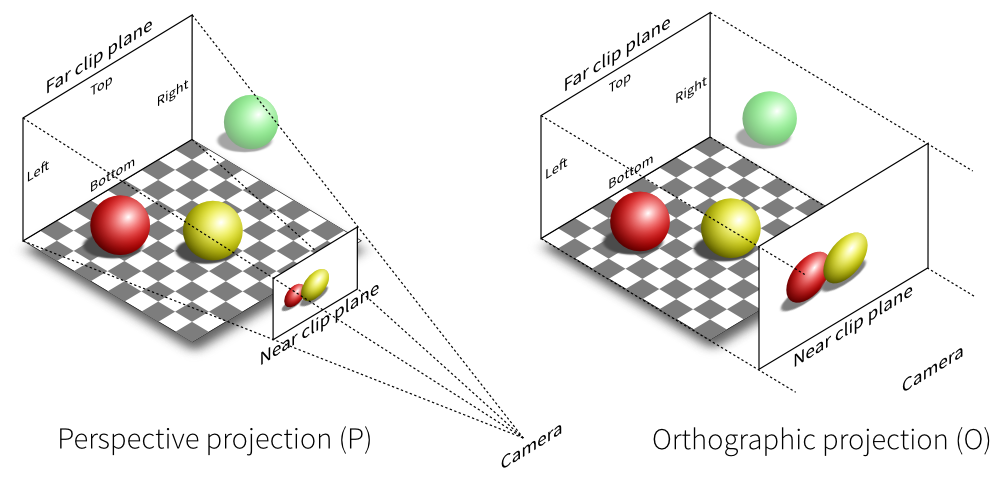
从图形学角度讲，透视投影将相机与被射平面组成一个四棱锥，将物体映射到中间的平面上，而正交投影假设相机在无限远处，这样相机与被射平面组成一个矩形，此时映射平面上的物体与真是物体的尺寸是相同的。

首先来说简单的正交投影，它非常好理解，将相机放在标准位置上，扔掉 ZZ 轴，得到的结果自然就是正交投影的结果。

假设点 pp 的坐标是 (2,4,−3)(2, 4, -3) ，扔掉 ZZ 轴坐标是 (2,4)(2, 4) ，正好就是它在 XYXY 平面上的位置。从侧面看，扔掉 ZZ 的坐标显然就是映射在 XYXY 平面上的坐标。

最后一步，将 XX 轴 YY 轴上覆盖图像的部分全都缩放到 −1-1 到 11 平面，也就是说不管图像在 XYXY 平面上有多大，全部给它缩放到 −1-1 到 11 上，这一步是为了方便之后的计算，也是约定俗成的，最终得到的结果就是正交投影的结果。

当然，上面只是直观上的理解，在图形学中正交投影是这么做的：将空间中的物体映射到标准立方体中 [−1,1]3[-1,1]^{3} 中，也就是下面的过程：

假设空间有一物体， l,r,t,b,n,fl,r,t,b,n,f 两个一组分别是在 XYZXYZ 轴上的值，这样就能定义出这个立方体的位置。首先将其变换到原点位置，然后将它缩放到标准立方体中，也就是中心是原点，变长为1的立方体中。写成矩阵形式就是

M=(2r−l00002t−b00002n−f00001)(100−r+l2010−t+b2001−n+f20001)M=\begin{pmatrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2}\\ 0 & 0 & 0 & 1 \end{pmatrix}

从矩阵可以看出，首先进行平移变换，矩阵乘积中右边的矩阵显然是一个平移矩阵，将矩形中心平移到原点处，之后进行缩放，将 XYZXYZ 轴覆盖的部分缩放为 −1-1 到 11 ，这里用2除是因为覆盖的范围是 −1-1 到 11 ，总和自然是2，除以两个点之间的差值，自然就是缩放到 −1-1 到 11 范围中了，这就是正交投影的过程。

接下来说透视投影，它比正交投影复杂些。先来回顾一个概念，三维坐标在齐次坐标体系下表示为

(xyz1)\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix}

其中的1的位置可以是一个任意不等于0的数，当它不为1时，齐次坐标表示为

(xwywzww),w≠0\begin{pmatrix} xw\\ yw\\ zw\\ w \end{pmatrix} ,w\neq 0

这与

(xyz1)\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix}

是完全相同的。那么既然两者相同， ww 可以是任意值，那么它与

(xzyzz2z),z≠0\begin{pmatrix} xz\\ yz\\ z^{2}\\ z \end{pmatrix} ,z\neq 0

也是完全相同的。例如 (1,0,0,1)(1, 0, 0, 1) 与 (2,0,0,2)(2, 0, 0, 2) 表示的都是 (1,0,0)(1, 0, 0) 。

与正交投影类似，透视投影中也有远近的概念

与正交投影的区别只是n与f的大小不同。透视投影过程中从f面到n面的过程实际上是在往里挤，也就是说f面的坐标都被缩放到n面的面积中，挤完之后再做一次正交投影，结果自然就是透视投影的结果，正交投影怎么做我们已经知道了，现在的问题就是这个挤的过程该如何表达。

在透视投影前首先得定义几条规则：

  • n面永远不变，在挤压过程中n面任意点永远不变
  • 挤压过程中f面任意点的z值不变（可以理解为挤压过程是f面单纯的向f面内收缩）
  • f面中心点不变

根据这几条规则，f面挤压的过程就是这样

从侧面观察挤压过程是这样的

中间的竖向虚线表示n面，右侧的竖向虚线表示f面，f面上某一点坐标为 (x,y,z)(x,y,z) ，挤压后坐标变为 (x′,y′,z′)(x^{\prime } ,y^{\prime } ,z^{\prime }) ，相机到n面的距离我们肯定是知道的，值为n，f面到相机的距离就是f面中坐标的z值，显然可以看出这里有一个相似三角形，那么就能得出f面挤压后映射在n面上的点的 y′y^{\prime } 值

y′=nzyy^{\prime } =\frac{n}{z} y

这个过程对于f面中任意一个点的挤压过程都是适用的，现在我们已经知道了f面挤压后的点的y坐标。同理对于x也可以得出

x′=nzxx^{\prime } =\frac{n}{z} x

使用齐次坐标表示，任意一个点

(xyz1)\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix}

经过某一挤压过程后都会变成

(nzxnzyunknown1)\begin{pmatrix} \frac{n}{z} x\\ \frac{n}{z} y\\ unknown\\ 1 \end{pmatrix}

这里z值为unknown是因为挤压过程不涉及z的变化（f面与n面的z不变），我们不关心z值到底是多少，结合透视变换开头说到的齐次坐标的规则，我们将坐标中的每一个值都乘以z，仍与原坐标相同，就是

(nxnyunknownz)\begin{pmatrix} nx\\ ny\\ unknown\\ z \end{pmatrix}

现在已经知道原始坐标和挤压后的坐标了，接着就能反推出挤压过程的矩阵，矩阵变换的过程为

M4×4(xyz1)=(nxnyunknownz)M^{4\times 4}\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} =\begin{pmatrix} nx\\ ny\\ unknown\\ z \end{pmatrix}

那么矩阵M就是

(n0000n00????0010)\begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ ? & ? & ? & ?\\ 0 & 0 & 1 & 0 \end{pmatrix}

在矩阵的第三行都是问号，这是因为在挤压后坐标的z值我们现在还是不知道的，但可以肯定的是它是根z有关系的。前面说过压缩的过程中n面与f面中的z不变，但从整个压缩过程来看，新点和旧点的z是变了。例如在n面中一点

(xyn1)\begin{pmatrix} x\\ y\\ n\\ 1 \end{pmatrix}

经过矩阵M变换后仍是

(xyn1)\begin{pmatrix} x\\ y\\ n\\ 1 \end{pmatrix}

同理f面的中也是，那么根据前面的

M4×4(xyz1)=(nxnyunknownz)M^{4\times 4}\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} =\begin{pmatrix} nx\\ ny\\ unknown\\ z \end{pmatrix}

我们将z替换为n，这一过程也就是

(xyn1)⟹(xyn1)=(nxnyn21)\begin{pmatrix} x\\ y\\ n\\ 1 \end{pmatrix} \Longrightarrow \begin{pmatrix} x\\ y\\ n\\ 1 \end{pmatrix} =\begin{pmatrix} nx\\ ny\\ n^{2}\\ 1 \end{pmatrix}

也就是说经过M变换后，坐标的第三行unknown我们知道了，就是 n2n^{2} ，那么矩阵M的第三行就能得到一半的信息

(00AB)\begin{pmatrix} 0 & 0 & A & B \end{pmatrix}

这是因为要想让结果的第三行为 n2n^{2} 不包括 xx 与 yy ，M的第三行前两列一定是0。但现在A与B仍有很多种可能将结果变为 n2n^{2} ，所以我们还需要一些信息来得出A与B。

刚才我们提过，透视变换的过程中n面与f面的中点相同，也就是说透视变换不会影响f面的中点，同样按照相面的过程，可以得出

(00f1)⟹(00f1)=(00f21)\begin{pmatrix} 0\\ 0\\ f\\ 1 \end{pmatrix} \Longrightarrow \begin{pmatrix} 0\\ 0\\ f\\ 1 \end{pmatrix} =\begin{pmatrix} 0\\ 0\\ f^{2}\\ 1 \end{pmatrix}

前两行为0是因为根据透视变换的原理，因为相机处于标准位置，那么f面中点就在x轴与y轴上。通过f面与n面两个变换规则可以得出两个式子

An+B=n2An+B=n^{2} Af+B=f2Af+B=f^{2}

最后就能得出

A=n+fA=n+f B=−nfB=-nf

到此为止，我们的挤压矩阵M就是

M4×4=(n0000n0000n+f−nf0010)M^{4\times 4}=\begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0 \end{pmatrix}

挤压矩阵结合正交投影矩阵，结果就是最终的透视投影矩阵

M透视=M正交M挤压M_{透视} =M_{正交} M_{挤压}

现在就可以将远处平面上的点投影到近处平面上了。